
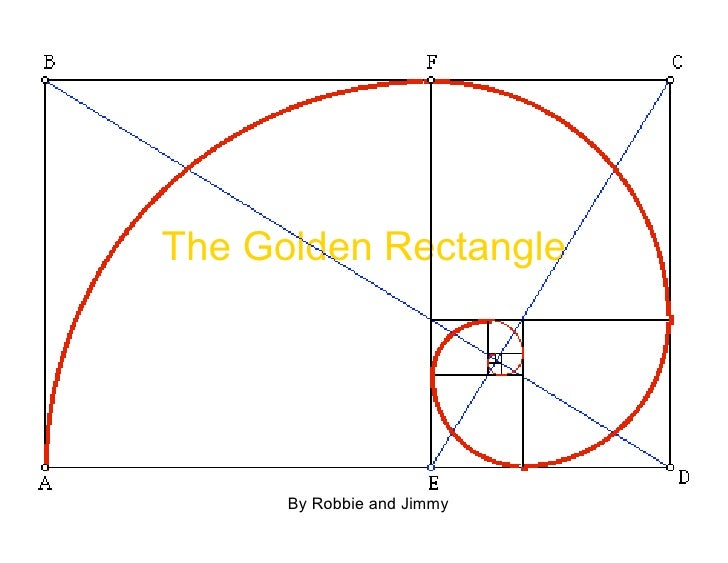
This quadrilateral figure contains sides that are in proportion to the golden ratio (their ratio and the ratio of the sum of two nonparallel sides to the larger of the parallel sides is equal to 1.618). One of the simplest constructions of the golden ratio is below. One of the greatest applications of the golden ratio in geometry is the golden rectangle.

Indeed most numbers between 1 and 2 will have two parts of the body approximating them in ratio. Golden ratios in the entablature of the Parthenon. The shadow-effect gives the table a minimalist appeal, but other color combinations will inspire different moods.1D Line, Circular Arc, Parabola, Helix, Koch Curve 2D Regular Polygons:Įquilateral Triangle, Square, Pentagon, Hexagon, Heptagon, Octagon, Nonagon, Decagon, Hendecagon, Dodecagon, Hexadecagon, N-gon, Polygon Ring If you look hard enough you will also find proportions in the human body close to 1.6, 5/3, 3/2, the square root of 2, 42/26, etc, etc. The Golden ratio has been used throughout our history in paintings, architecture, and even music more aesthetically pleasing to the human eye. This coffee table is made from welded and powder coated steel with inset, smoked black glass. Use that line as the radius to draw an arc that defines the height of the rectangle. Draw a line from the midpoint of one side of the square to an opposite corner.ģ. In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, which is 1: (or phi, approx 1.618).
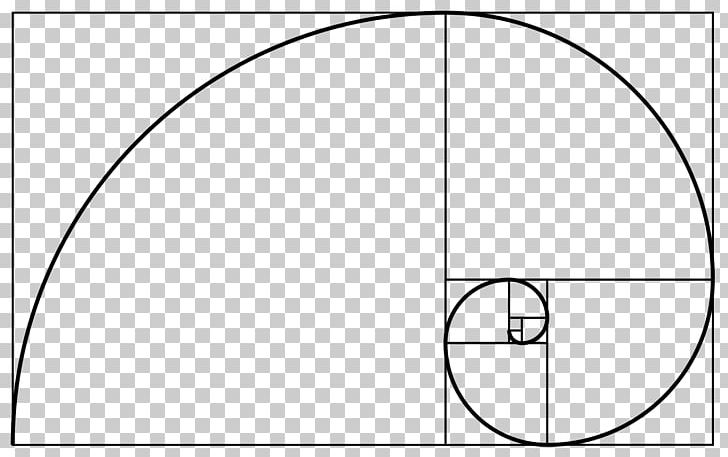
It is famously said to have great aesthetic appeal and is closely. It is created by these simple instructions:Ģ. The golden ratio, as we have seen also appears many times in the regular pentagon and its pentagram of diagonals. The so-called golden rectangle is one whose sides a and b stand in the golden ratio. This ratio is often referred to as the Fibonacci Sequence in nature. Considered the Father of Accounting and Bookkeeping, he was a contemporary of Leonardo Da Vinci. A rectangle whose dimensions obey the Golden Ratio is called a Golden Rectangle. It was ultimately popularized by Italian mathematician Fra Luca Bartolomeo de Pacioli in the 15th Century. These rectangles are called golden rectangles.

The golden rectangle has an interesting property: if you divide it into a square with the side equal to the rectangle’s shorter dimension and another rectangle (like in the image below), it turns out that the smaller rectangle is a golden rectangle as well. During the 5th Century BC, Egyptian mathematician Euclid studied and obsessed over these proportions. Hence, the new rectangle in blue has the same ratio of the large side to the small side as the original one. The golden rectangle has sides that are in the golden ratio (a/b ). What is the Golden Ratio Uses of the Fibonacci Sequence Lesson Summary What is the Fibonacci Sequence The Fibonacci sequence is the sequence of numbers given by 1, 1, 2, 3, 5, 8, 13. The origin of the ratio is unclear and some have found it dates back to the ancient Egyptians and the construction of their pyramids. This ratio is found in some patterns in nature and is how many artists have composed their works. Definition The Golden Ratio is an irrational number, approximately 1.618, which is prevalent in nature, art, architecture, and design. The smaller rectangle has sides with ratio 1-x : 1 since this is the same as the ratio for the big rectangle, one finds that x2 x+1 and thus x (1+Sqrt(5))/. In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, which is 1:Φ (or "phi", approx 1.618).


 0 kommentar(er)
0 kommentar(er)
